Comprenda y resuelva triángulos rectángulos con facilidad
La Calculadora de Triángulos Rectángulos es una herramienta imprescindible para estudiantes, profesores, ingenieros y aficionados a las matemáticas. Los triángulos rectángulos son fundamentales en geometría, y aparecen en todo, desde la arquitectura y la navegación hasta la física y la trigonometría básica. Resolverlos puede ser sencillo si se tienen las herramientas adecuadas.
Ya sea que busques la hipotenusa, un ángulo faltante o la longitud de un lado, nuestra calculadora te ofrece resultados instantáneos utilizando el teorema de Pitágoras y los principios trigonométricos. En esta guía, aprenderás cómo funciona, por qué es útil y cómo explorar calculadoras relacionadas para fortalecer tus habilidades de resolución de problemas matemáticos.
¿Qué es un triángulo rectángulo?
Un triángulo rectángulo es un triángulo con un ángulo de 90 grados. Está compuesto por:
Dos patas : Los lados que forman el ángulo recto.
Una hipotenusa : El lado más largo, opuesto al ángulo recto.
Dos ángulos agudos : siempre suman 90°.
Comprender estas partes le permitirá aplicar varias reglas matemáticas como el teorema de Pitágoras o las razones seno, coseno y tangente.
Cómo funciona la calculadora de triángulos rectángulos
Nuestra calculadora utiliza principios geométricos y trigonométricos estándar para resolver cualquier triángulo rectángulo. Simplemente introduce cualquier combinación de lados o ángulos y calcula el resto.
Entradas clave:
Longitud de dos lados cualesquiera (por ejemplo, el cateto y la hipotenusa)
Un ángulo y un lado
Seno, coseno o tangente si se utiliza trigonometría
Detrás de escena, utiliza:
Teorema de Pitágoras : a² + b² = c²
Razones trigonométricas : sin(θ) = opuesto/hipotenusa, etc.
Pruébelo ahora con la herramienta completa: Calculadora de triángulos rectángulos .
Aplicaciones de los triángulos rectángulos en el mundo real
Los triángulos rectángulos están en todas partes en la vida real:
Construcción y arquitectura : Para garantizar que las estructuras estén niveladas o medir la pendiente.
Navegación y GPS : para determinar las distancias más cortas.
Física e Ingeniería : En análisis de vectores de fuerza o cálculo de ángulos de inclinación.
Diseño y Arte : Crear patrones proporcionales y escalables.
Entender cómo resolver estos triángulos no es sólo académico: es práctico.
Ejemplo paso a paso usando la calculadora
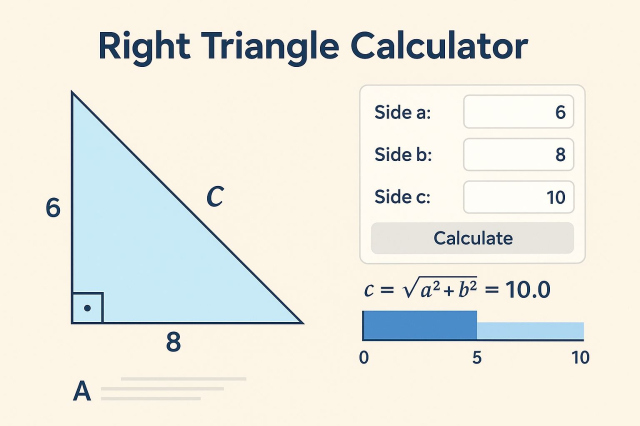
Imagina que sabes que un cateto mide 6 cm y el otro 8 cm. Quieres hallar la hipotenusa:
Lado de entrada A = 6, lado B = 8.
La calculadora aplica el teorema de Pitágoras:
√(6² + 8²) = √(36 + 64) = √100 = 10
Resultado: Hipotenusa = 10 cm
También puedes cambiar al modo de ángulo y encontrar el ángulo usando funciones trigonométricas.
Explora otras calculadoras matemáticas útiles
Nuestra plataforma ofrece más herramientas para profundizar su comprensión:
🔺 Calculadora del Teorema de Pitágoras – Resuelve directamente la famosa ecuación a² + b² = c².
📐 Calculadora de trigonometría : calcula seno, coseno y tangente para cualquier ángulo o triángulo.
📏 Calculadora de área : encuentra el área de un triángulo, rectángulo, círculo y más.
🔬 Calculadora científica : realiza operaciones matemáticas complejas en un solo lugar.
Estas herramientas funcionan juntas a la perfección, ahorrando tiempo y mejorando la precisión.
Resolver triángulos rectángulos al instante
Las matemáticas ya no tienen por qué ser un problema. Con la Calculadora de Triángulos Rectángulos , puedes resolver cualquier triángulo rectángulo en segundos. Olvídate de cálculos manuales y de tener que volver a intentar resolver tus fórmulas: solo resultados claros y precisos al instante.
Úsalo para tus tareas, exámenes, planos de construcción o para resolver problemas diarios. Combínalo con nuestro conjunto de herramientas matemáticas para cubrir todas tus necesidades geométricas.
Preguntas frecuentes (FAQ)
¿Cómo se encuentra la hipotenusa de un triángulo rectángulo?
Utilice el teorema de Pitágoras: a² + b² = c².
¿Qué fórmulas utiliza la calculadora?
Utiliza el teorema de Pitágoras y trigonometría básica (sin, cos, tan).
¿Esta herramienta también puede resolver ángulos?
Sí, si ingresa las longitudes de los lados, puede calcular los ángulos utilizando razones trigonométricas.
¿Esta calculadora es adecuada para estudiantes de secundaria?
Por supuesto. Es fácil de usar y cumple con los estándares curriculares.
¿Puedo usarlo en el móvil?
Sí, la calculadora es totalmente responsiva y compatible con dispositivos móviles.