Understand and Solve Right Triangles with Ease
The Right Triangle Calculator is a must-have tool for students, teachers, engineers, and math enthusiasts. Right-angled triangles are fundamental in geometry, appearing in everything from architecture and navigation to physics and basic trigonometry. Solving one can be simple — if you have the right tools.
Whether you're trying to find the hypotenuse, a missing angle, or a side length, our calculator delivers instant results using the Pythagorean theorem and trigonometric principles. In this guide, you'll learn how it works, why it's useful, and how to explore related calculators to strengthen your math problem-solving skills.
What Is a Right Triangle?
A right triangle is a triangle with one 90-degree angle. It consists of:
-
Two legs: The sides that form the right angle.
-
One hypotenuse: The longest side, opposite the right angle.
-
Two acute angles: Always adding up to 90°.
Understanding these parts allows you to apply various mathematical rules like the Pythagorean theorem or sine, cosine, and tangent ratios.
How the Right Triangle Calculator Works
Our calculator uses standard geometry and trigonometric principles to solve any right-angled triangle. You simply input any combination of sides or angles, and it computes the rest.
Key Inputs:
-
Length of any two sides (e.g., leg and hypotenuse)
-
One angle and one side
-
Sine, cosine, or tangent if using trigonometry
Behind the scenes, it uses:
-
Pythagorean Theorem: a² + b² = c²
-
Trigonometric Ratios: sin(θ) = opposite/hypotenuse, etc.
Try it now with the full tool: Right Triangle Calculator.
Real-World Applications of Right Triangles
Right-angled triangles are everywhere in real life:
-
Construction & Architecture: To ensure structures are level or measure slope.
-
Navigation & GPS: For determining shortest distances.
-
Physics & Engineering: In force vector analysis or calculating incline angles.
-
Design & Art: To create proportional, scalable patterns.
Understanding how to solve these triangles isn't just academic — it's practical.
Step-by-Step Example Using the Calculator
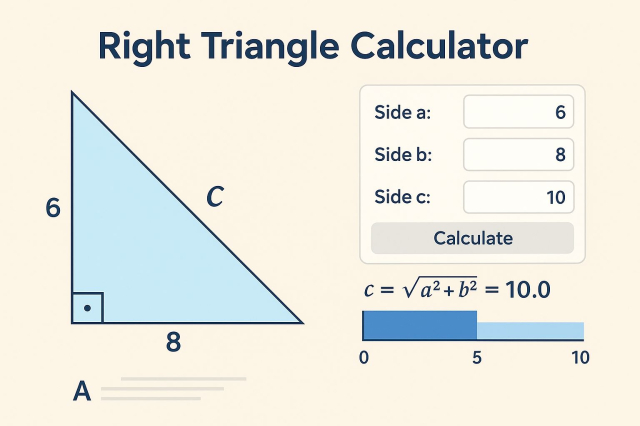
Imagine you know one leg is 6 cm and the other is 8 cm. You want to find the hypotenuse:
-
Input side A = 6, side B = 8.
-
The calculator applies the Pythagorean theorem:
-
√(6² + 8²) = √(36 + 64) = √100 = 10
-
-
Result: Hypotenuse = 10 cm
You can also switch to angle mode and find the angle using trigonometric functions.
Explore Other Useful Math Calculators
Our platform offers more tools to deepen your understanding:
-
🔺 Pythagorean Theorem Calculator – Directly solve the famous equation a² + b² = c².
-
📐 Trigonometry Calculator – Calculate sin, cos, tan for any angle or triangle.
-
📏 Area Calculator – Find the area of a triangle, rectangle, circle, and more.
-
🔬 Scientific Calculator – Perform complex mathematical operations all in one place.
These tools work seamlessly together, saving time and boosting accuracy.
Solve Right Triangles Instantly
Math doesn't need to be a struggle. With the Right Triangle Calculator, you can solve any right-angled triangle in seconds. No more manual calculations or second-guessing your formulas — just clear, accurate results, instantly.
Use it for your homework, exams, construction plans, or daily problem-solving. Combine it with our suite of math tools for full coverage of your geometric needs.
Frequently Asked Questions (FAQ)
How do you find the hypotenuse of a right triangle?
Use the Pythagorean theorem: a² + b² = c².
What formulas does the calculator use?
It uses the Pythagorean theorem and basic trigonometry (sin, cos, tan).
Can this tool solve for angles too?
Yes, if you input side lengths, it can compute the angles using trigonometric ratios.
Is this calculator suitable for high school students?
Absolutely. It's user-friendly and follows curriculum standards.
Can I use it on mobile?
Yes, the calculator is fully responsive and mobile-friendly.